마케팅에서 예측(forecasting)은 수요나 매출 예측 등 거시적인 목적으로도 많이 쓰이지만, 개인적으로는 단기적인 마케팅 캠페인의 효과를 측정하기 위한 여러가지 방법을 고민하면서 예측 기법에 대해 더 깊은 관심을 갖게 되었다. 예측을 활용한 효과 측정의 논리를 거칠게 말하자면 예측 기법을 통해 ‘synthetic control’이라는 조건법적(counterfactual) 결과를 만들어 실제 결과와 비교하는 것이다(e.g., 이 캠페인을 하지 않았더라면 vs. 실제로 이 캠페인을 했더니).

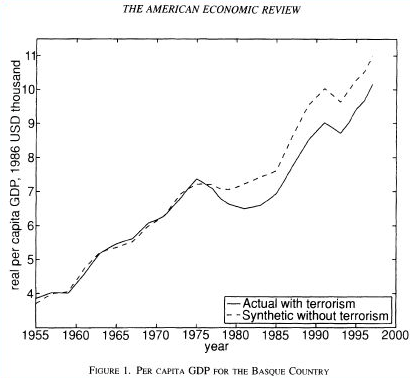
Figure 1. Synthetic Control (source: World Bank Blog)

   이와 관련하여 마케터들에게 가장 널리 알려진 방법론은 2015년에 구글에서 발표한 CausalImpact일 것이다. 이 방법론은 ‘Bayesian structural time-series models’에 기반하여 synthetic control을 만들어 주는데, 원리를 정확히 이해하지 못하더라도 배포되어있는 R패키지를 이용하여 누구나 결과값을 만들어 낼 수는 있다. 현재 근무 중인 회사에서도 이 패키지를 Shiny 웹앱으로 배포하여 누구나 사용할 수 있도록 하고 있는데, 이 방법론에 대한 생각은 (모델에 대한 공부를 더 한 이후에..) 추후 별도 포스팅에서 정리하고자 한다. 그 다음으로는 ‘Forecasting at scale’을 주창하며 페이스북에서 2017년에 발표한 Prophet이 있을 것이다. Prophet은 시계열 데이터를 ‘Growth + Seasonality + Holidays + Error’의 additive한 모델로 인식하여 필자와 같이 통계적 지식이 부족한 사용자도 파라미터들을 보다 직관적으로 이해하고 조정하면서 사용할 수 있도록 만들어놨다. 실제로 회사에서도 많은 사람들이 Prophet 패키지를 애용하고 있다. 그 외에 결과값을 만들기 가장 쉬운 방법으로는 태블로(Tableau)의 built-in forecasting이 있을 것 같다. 이 방법은 ‘Exponential Smoothing(지수평활법)’에 근거하는데 그 성능과 설명의 용이성을 차치하고 클릭 몇 번으로 예측값을 제조(?)할 수 있는 것이 가장 큰 강점이다. 마지막으로 YoY를 이용하는 가장 원시적인 방법이 있는데 전년 데이터가 없을 경우 사용할 수 없고 ‘어느 시점의 어떤 YoY’를 이용하는 것이 가장 적절한지 평가하기 어렵다는 치명적인 단점을 갖고 있다.

   그러나 이처럼 상대적으로 접근이 용이한 방법론들을 살펴보기 전에, 본 포스팅에서는 먼저 ARIMA(Auto-Regressive Integrated Moving Average)라는 그 유래가 1930년대까지 거슬러 올라가는 클래식(?)한 시계열 예측 모델을 파이썬으로 적용하고 구현하는 방법에 대해서 정리하고자 한다.

1.Decomposition

   먼저 예측에 사용하고 싶은 데이터를 Pandas DataFrame형태로 가공한 것을 전제로 한다. 여기서는 한국공항공사에서 2000년 1월부터 2020년 1월까지의 월별 여객 출국자 수를 불러왔다. 그리고 statsmodels 패키지에서 seasonal_decompose를 불러와 준비한 데이터를 decompose해보도록 한다.

from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(df['Travellers'], freq=12)
fig = plt.figure()
fig = decomposition.plot()
fig.set_size_inches(16,9)

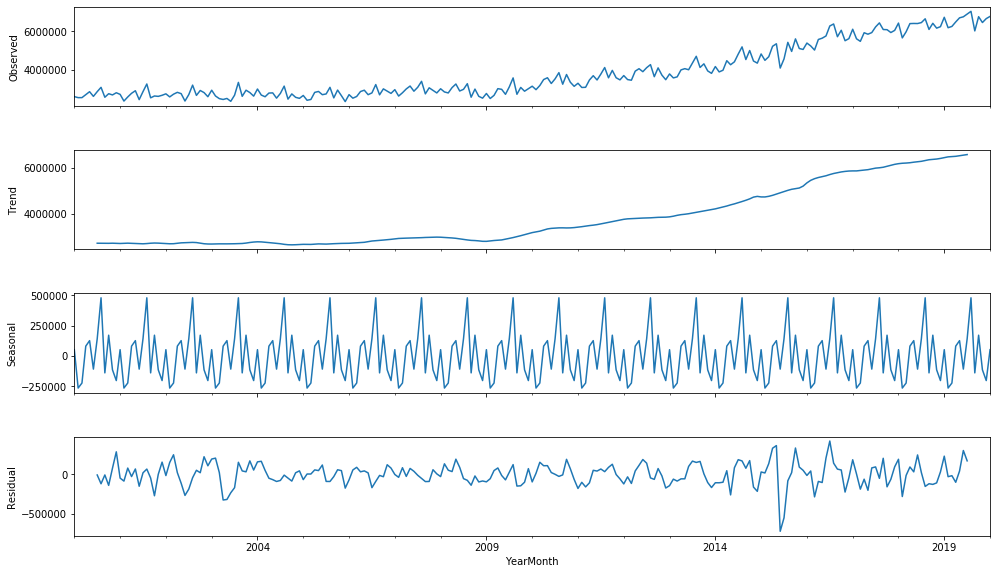
   여기서 우리는 이 데이터가 월별 출국자 숫자이기 때문에 해당 데이터에 seasonality가 있을 것이라고 쉽게 예상할 수 있다. 여기서는 그러한 seasonality가 1년 단위로 반복되는 경향이 있다고 추측했기 때문에 ‘freq=12’로 설정했고, 따라서 위의 3번째 그래프에서 12개월 단위로 decompose된 seasonality를 볼 수 있다. 데이터에 주별, 분기별 등의 경향이 있다고 예상하는 경우 freq 파라미터를 적절하게 조정해주면 된다.

2.Stationarity

   ARIMA 모델 학습에 있어서 중요한 부분은 시계열 데이터가 평균과 분산, 그리고 공분산이 일정한 정상성(Stationarity)을 갖추고 있는지를 먼저 검증하는 것이다. 여기서 우리의 월별 출국자 데이터는 해가 지날수록 우상향하는 추세를 보이므로 정상성을 갖추고 있다고 볼 수 없고, 이를 위해 뒤에서 차분(differencing)이라는 방법을 통해 시계열 데이터가 정상성을 나타내도록 처리할 것이다. 지금 단계에서는 일단 ‘Augemented Dickey-Fuller Unit Root Test’ 라는 함수를 통해 정상성을 검증하도록 하자. statsmodels의 adfuller가 바로 그 함수인데 테스트 결과값을 읽기 쉽게 표시해주지 않기 때문에 하기와 같이 별도의 함수로 만들어줬다. 이 함수는 후에 Differencing 단계에서 여러번 쓰이게 된다.

from statsmodels.tsa.stattools import adfuller

def adfuller_test(data):
    result = adfuller(data)
    print('Augmented Dickey-Fuller Unit Root Test:')
    labels = ['Test Statistic', 'p-value', 'Number of Lags', 'Number of Obsevations']
    
    for value,label in zip(result,labels):
        print(label+' : '+str(value))
        
    if result[1] <= 0.05:
        print("Reject the null hypothesis. Data has no unit root and is stationary")
    else: 
        print("Time series has a unit root, indicating it is non-stationary")

3.Differencing

   뒤에서 Seasonal ARIMA 모델을 학습시킬 때 하기와 같이 함수를 적용하게 되는데 여기서 우리는 p,d,q 그리고 P,D,Q,S라는 파라미터를 지정해줘야 한다.

model = sm.tsa.statespace.SARIMAX(df['Travellers'],order=(p,d,q), seasonal_order=(P,D,Q,S))

   p는 AR(Auto-Regressive) 파라미터를, 그리고 q는 MA(Moving Average)파라미터를 의미하고 d는 정상성을 찾기위해 몇 번의 lag를 써서 Differencing 해주었는지를 의미하는 파라미터이다. 대문자 P,D,Q는 같은 의미의 파라미터인데 Seasonal Differencing을 통해 찾은 파라미터 값들을 적용하면 되고, S는 우리가 설정한 Seasonality 주기를 의미한다(여기서는 12). 이제 한 lag씩 Differencing 해보면서 적절한 d와 D값을 찾아보도록 하자.

#Differencing
df['Travellers 1st Diff'] = df['Travellers'] - df['Travellers'].shift(1)
df['Travellers 2nd Diff'] = df['Travellers 1st Diff'] - df['Travellers 1st Diff'].shift(1)

#Seasonal Differencing
df['Seasonal Diff'] = df['Travellers'] - df['Travellers'].shift(12)
df['Seasonal 1st Diff'] = df['Travellers 1st Diff'] - df['Travellers 1st Diff'].shift(12)

#1st Differncing adfuller test
adfuller_test(df['Travellers 1st Diff'].dropna())

#1st Seasonal Differencing 
adfuller_test(df['Seasonal 1st Diff'].dropna())

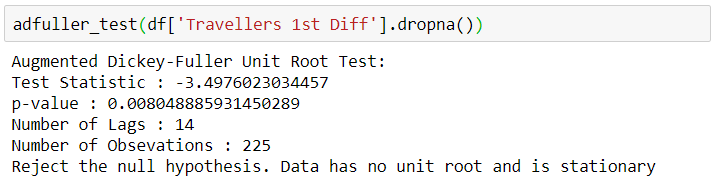
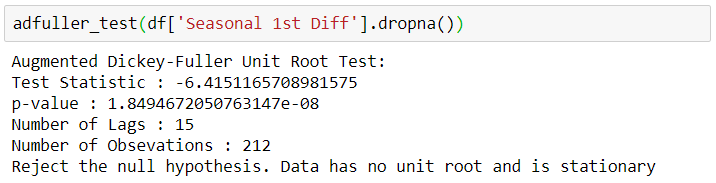
   adfuller test 결과 lag 1 Differencing에서, 또 lag 1 Seasonal Differencing에서 정상성(Stationarity)이 인정된다. 따라서 d=1, D=1로 파라미터 값을 지정할 수 있다.

4.ACF/PACF Interpretation

   이제 적절한 p,q,P,Q의 값을 찾아야 하는데, 이 페이지에 다소 복잡한 Rule of Thumb이 잘 정리되어있다. 이를 모두 이해하기 전에 우선 ACF(Auto-Correlation Function)와 PACF(Partial Auto-Correlation Function)을 통해 lag에 따른 Correlation을 그래프로 확인해보자.

figure, ((ax1, ax2)) = plt.subplots(nrows=1, ncols=2)
figure.set_size_inches(16,6)
ax1 = plot_acf(df["Travellers 1st Diff"].dropna(), ax=ax1)
ax2 = plot_pacf(df["Travellers 1st Diff"].dropna(), ax=ax2)

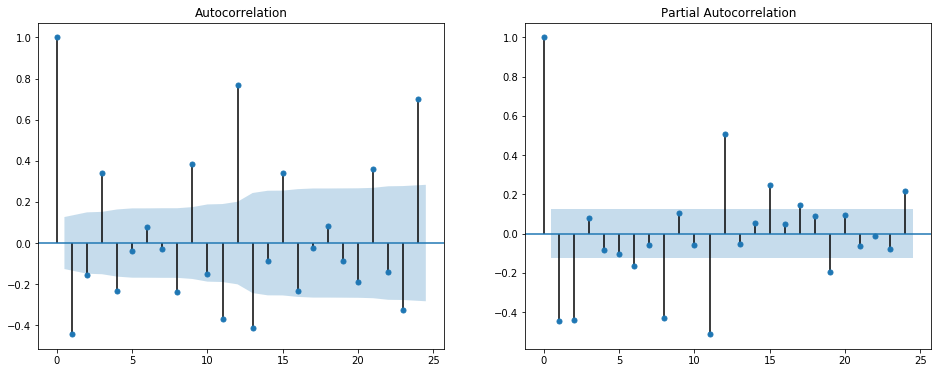
figure, ((ax1, ax2)) = plt.subplots(nrows=1, ncols=2)
figure.set_size_inches(16,6)
ax1 = plot_acf(df["Seasonal 1st Diff"].dropna(), ax=ax1)
ax2 = plot_pacf(df["Seasonal 1st Diff"].dropna(), ax=ax2)

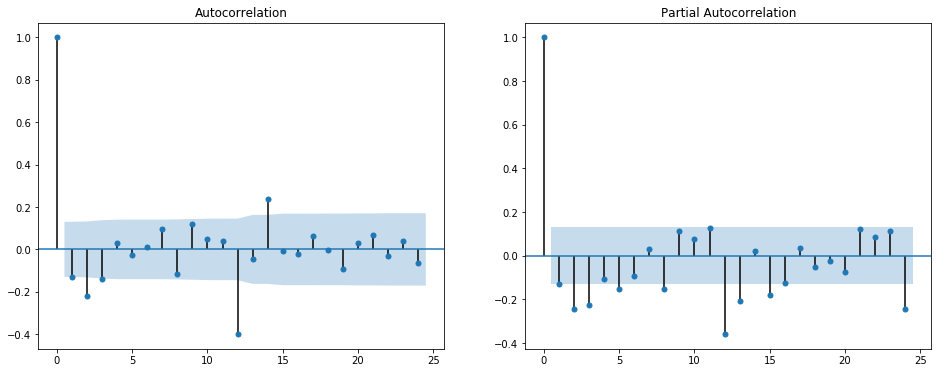
   일반적으로 AR(p) 파라미터는 PACF로, MA(q) 파라미터는 ACF로 결정할 수 있다고 하는데, 시각화로만 이 파라미터 값들을 결정하기 어려운 경우도 많은 것으로 보인다. 현재 데이터에서도 ‘Seasonal 1st Differencing’의 경우 PACF와 ACF 모두 lag 12에 높은 Correlation을 나타내는 것으로 보아 P=1, Q=1으로 설정하는게 무난할 것으로 보이지만, 충분히 만족스러운 설명은 아니다(파라미터 튜닝과 그 함의에 대해서는 추후에 별도 포스팅에서 다뤄보고자 한다). ‘Travellers 1st Differencing’의 경우에는 파라미터를 결정하기가 더욱 애매하다. PACF에서는 1,2,8,11 등의 lag에서, ACF에서도 1,3,9 등의 lag에서 Correlation이 두드러진다. 이런 경우에는 여러가지 파라미터 조합으로 모델을 만들어 각 모델의 AIC(Akaike Information Criterion)와 BIC(Bayesian Information Criterion)를 비교하여 가장 그 수치가 낮은 모델의 파라미터 조합을 선택하는 방법을 쓴다고 한다. AIC와 BIC 수치는 ARIMA 모델 결과값에 나오므로, 그 수치들을 비교할 수 있게 다음과 같이 ‘For’ iteration을 만들었다.

import itertools

d = range(1, 2)
p = q = range(0, 3)
pdq = list(itertools.product(p, d, q))
#P,D,Q,S의 경우에는 위에서 각각 1,1,1,12로 결정

for param in pdq:
        try:
            mod = sm.tsa.statespace.SARIMAX(df['Travellers'],order=param,seasonal_order=(1,1,1,12))
            results = mod.fit()
            print('ARIMA{}x{}12 - AIC:{} - BIC {}'.format(param,param_seasonal,results.aic,results.bic))
        except: 
            continue;

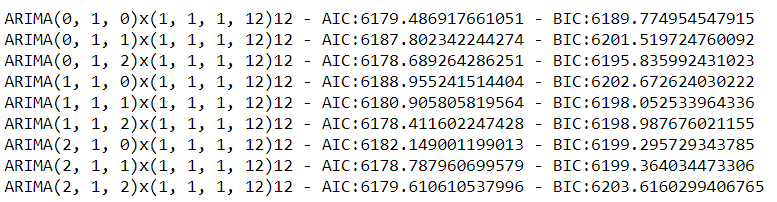
   이제 파라미터 조합별 AIC, BIC 수치를 비교할 수 있게 되었다. 본 포스팅에서는 AIC와 BIC 수치가 함께 상대적으로 낮은 파라미터 조합((p,d,q)=(0,1,2))을 골라 모델을 학습시켰지만, 모델을 더 잘 설명하기 위해서는 여러가지 파라미터 조합을 비교해보면서 결정하는 것이 좋다.

5.Seasonal ARIMA

model = sm.tsa.statespace.SARIMAX(df['Travellers'],order=(0,1,2), seasonal_order=(1,1,1,12))
results = model.fit()
print(results.summary())

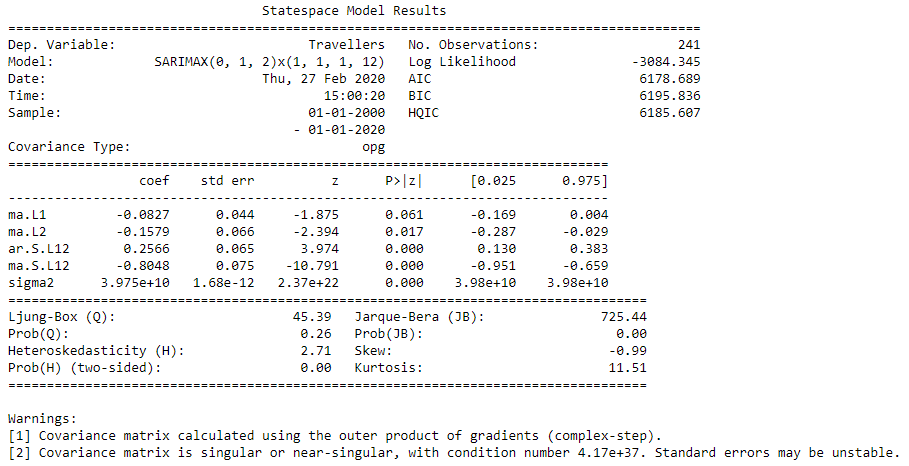
   위와 같이 모델을 학습시킨 결과를 확인할 수 있는데, 여기서 파라미터별 coefficient와 ‘p-value <0.05’ 여부도 알 수 있다. 또한 하기와 같이 plot_diagnostics 함수를 이용하면 추가적으로 residual에 대한 검증을 할 수 있다.

results.plot_diagnostics(figsize=(16, 8))
plt.show()

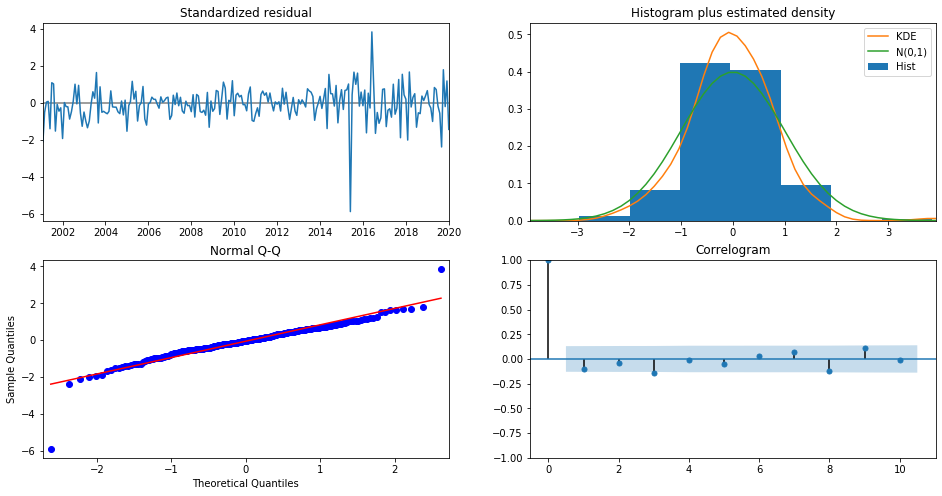
   정규화(standardize)시킨 residual이 가우시안 분포를 따르는지, 자기상관성이 없는지 등의 여부를 이렇게 확인이 가능하다. 2사분면의 그래프를 보면 2015년과 2017년에 residual이 크게 튀는 부분이 있는데 이때 급격한 출국자수 증감이 있었던 것으로 보인다. 그럼 이제 실제 데이터와 얼마나 fit하는지 살펴보도록 하자.

df['forecast'] = results.predict(start = 218, end= 241, dynamic= True)  
df[['Travellers','forecast']].plot(figsize=(12,8))

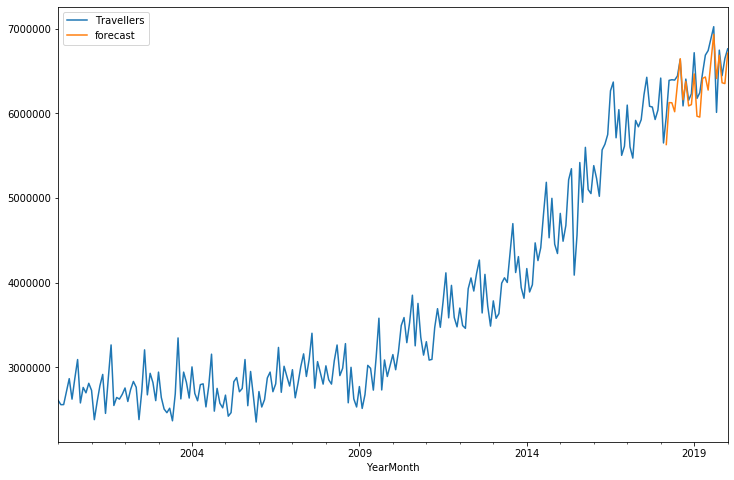
   추세에 공통점이 있지만 2년 간의 데이터를 예측하도록 했더니 월별 격차가 꽤 생겨나는 것을 볼 수 있다. 당연한 이야기지만 예측하는 기간을 줄이면 정확도는 올라간다. 이제 DataFrame에 ‘미래의 연월’ Index를 추가하여 Forecasting 라인을 그려보자.

#추가 Index 생성
from pandas.tseries.offsets import DateOffset

future_dates = [df.index[-1] + DateOffset(months=x) for x in range(0,24) ]
future_dates_df = pd.DataFrame(index=future_dates[1:],columns=df.columns)
future_df = pd.concat([df,future_dates_df])

#Forecast
future_df['forecast'] = results.predict(start = 218, end = 265, dynamic= True)  
future_df[['Travellers', 'forecast']].plot(figsize=(12, 8)) 

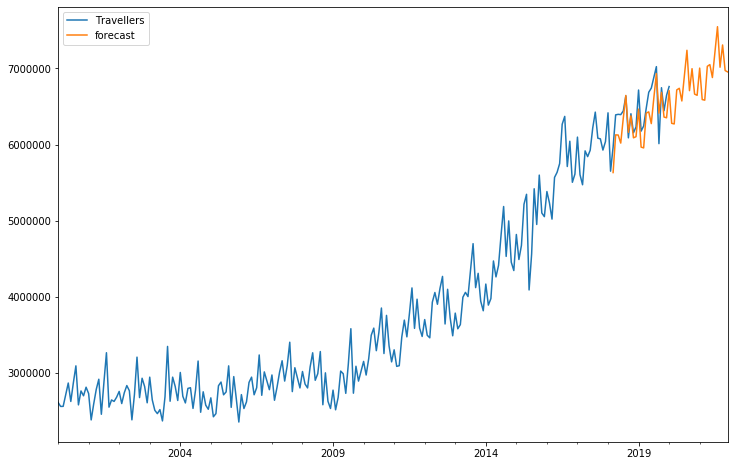
   이 예측은 얼마나 맞을까? 일단 COVID-19 바이러스로 인해 2월 예측치부터 엄청나게 틀릴 것이라고 본다. ARIMA는 근본적으로 시간에 따른 자기상관성(Auto-Regression), 시계열 데이터의 정상성(Stationarity), 잔차의 이동평균(Moving Average)을 활용한 예측 모델이므로 이러한 Black Swan을 예측하기에는 한계가 분명하다(다른 예측모델도 마찬가지겠지만). 뿐만 아니라 음력을 따르는 휴일, 성장 추세 등을 반영하기에도 어려움이 있을 것이다. 그러나 다른 예측 모델을 활용하기에 앞서 ARIMA가 대략적으로 어떻게 작동하는지를 이해하는 것이 추후에 적절한 모델 선택을 하는데 도움이 될거라 생각한다.

   ARIMA 모델 하나에도 이미 많은 통계적 개념과 함의가 들어있기 때문에 여러가지 구현 사례를 보면서도 이해하기 어려운 부분이 많았다. 특히 파라미터 선택과 튜닝에 대해서는 여러가지 형태의 데이터로 모델링해보면서 ARIMA에 전반에 대한 이해를 끌어올리는 과정이 필요할 것 같다. 모델과 예측 결과값에 대한 평가에 있어서도 다른 방법론들을 찾아서 구현해보고 추후 별도의 포스팅으로 업데이트하고자 한다.